Insertion Sort : Algorithm and Pseudo Code
Insertion sort is a simple sorting algorithm: a comparison sort in which the sorted array (or list) is built one entry at a time. Every repetition of insertion sort removes an element from the input
data, inserting it into the correct position in the already-sorted list,
until no input elements remain. The choice of which element to remove
from the input is arbitrary, and can be made using almost any choice
algorithm.
Sorting is typically done in-place. The resulting array after k iterations has the property where the first k + 1 entries are sorted. In each iteration the first remaining entry of the input is removed, inserted into the result at the correct position, thus extending the result.
The best case input is an array that is already sorted. In this case insertion sort has a linear running time (i.e., O(n)). The worst case input is an array sorted in reverse order. In this case every iteration of the inner loop will scan and shift the entire sorted subsection of the array before inserting the next element. For this case insertion sort has a quadratic running time (i.e., O(n2)). The average case is also quadratic, which makes insertion sort impractical for sorting large arrays.
However, insertion sort is one of the fastest algorithms for sorting very small arrays, even faster than quicksort; indeed, good quicksort implementations use insertion sort for arrays smaller than a certain threshold, also when arising as sub-problems; the exact threshold must be determined experimentally and depends on the machine, but is commonly around ten.
Insertion sort is very similar to selection sort. As in selection sort, after k passes through the array, the first k elements are in sorted order. For selection sort these are the k smallest elements, while in insertion sort they are whatever the first k elements were in the unsorted array. Insertion sort's advantage is that it only scans as many elements as needed to determine the correct location of the k+1st element, while selection sort must scan all remaining elements to find the absolute smallest element.
Calculations show that insertion sort will usually perform about half as many comparisons as selection sort. Assuming the k+1st element's rank is random, insertion sort will on average require shifting half of the previous k elements, while selection sort always requires scanning all unplaced elements. If the input array is reverse-sorted, insertion sort performs as many comparisons as selection sort. If the input array is already sorted, insertion sort performs as few as n-1 comparisons, thus making insertion sort more efficient when given sorted or "nearly-sorted" arrays.
While insertion sort typically makes fewer comparisons than selection sort, it requires more writes because the inner loop can require shifting large sections of the sorted portion of the array. In general, insertion sort will write to the array O(n2) times, whereas selection sort will write only O(n) times. For this reason selection sort may be preferable in cases where writing to memory is significantly more expensive than reading, such as with EEPROM or flash memory.
Pseudo Code :
InsertionSort(A){
for j = 2 to length(A){
key = A[j];
// Insert A[j] into sorted sequence A[1..j-1]
i = j-1;
while(i > 0 && A[i] > key){
A[i+1] = A[i];
i--;
}
A[i+1] = key;
}
}
Sorting is typically done in-place. The resulting array after k iterations has the property where the first k + 1 entries are sorted. In each iteration the first remaining entry of the input is removed, inserted into the result at the correct position, thus extending the result.
The best case input is an array that is already sorted. In this case insertion sort has a linear running time (i.e., O(n)). The worst case input is an array sorted in reverse order. In this case every iteration of the inner loop will scan and shift the entire sorted subsection of the array before inserting the next element. For this case insertion sort has a quadratic running time (i.e., O(n2)). The average case is also quadratic, which makes insertion sort impractical for sorting large arrays.
However, insertion sort is one of the fastest algorithms for sorting very small arrays, even faster than quicksort; indeed, good quicksort implementations use insertion sort for arrays smaller than a certain threshold, also when arising as sub-problems; the exact threshold must be determined experimentally and depends on the machine, but is commonly around ten.
Insertion sort is very similar to selection sort. As in selection sort, after k passes through the array, the first k elements are in sorted order. For selection sort these are the k smallest elements, while in insertion sort they are whatever the first k elements were in the unsorted array. Insertion sort's advantage is that it only scans as many elements as needed to determine the correct location of the k+1st element, while selection sort must scan all remaining elements to find the absolute smallest element.
Calculations show that insertion sort will usually perform about half as many comparisons as selection sort. Assuming the k+1st element's rank is random, insertion sort will on average require shifting half of the previous k elements, while selection sort always requires scanning all unplaced elements. If the input array is reverse-sorted, insertion sort performs as many comparisons as selection sort. If the input array is already sorted, insertion sort performs as few as n-1 comparisons, thus making insertion sort more efficient when given sorted or "nearly-sorted" arrays.
While insertion sort typically makes fewer comparisons than selection sort, it requires more writes because the inner loop can require shifting large sections of the sorted portion of the array. In general, insertion sort will write to the array O(n2) times, whereas selection sort will write only O(n) times. For this reason selection sort may be preferable in cases where writing to memory is significantly more expensive than reading, such as with EEPROM or flash memory.
Pseudo Code :
InsertionSort(A){
for j = 2 to length(A){
key = A[j];
// Insert A[j] into sorted sequence A[1..j-1]
i = j-1;
while(i > 0 && A[i] > key){
A[i+1] = A[i];
i--;
}
A[i+1] = key;
}
}
| Worst case performance | : О(n2) |
|---|---|
| Best case performance | : O(n) |
| Average case performance | : О(n2) |
| Worst case space complexity | : О(n) total, O(1) auxiliary |
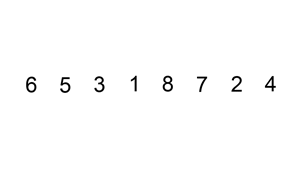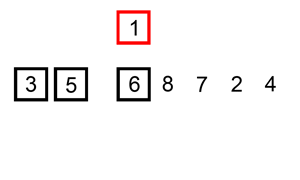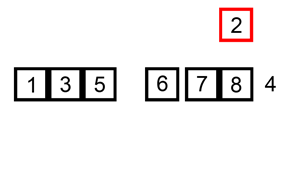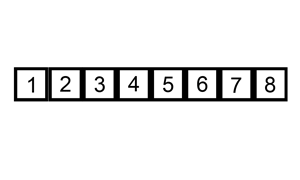


Comments
Post a Comment